2 & 3 Dimensions - Higher Dimensions
Note: This page contains excerpts from the Multi-Dimensional Geometry Digital Book. Click here to go to the Book Page to get it.
Mathematics from Greek (μάθημα) máthēma, - knowledge, study, learning - is the study of topics such as quantity (numbers), structure, space, and change.
Geometry (from the Ancient Greek: (γεωμετρία); geo - “earth”, -metron “measurement”) is a branch of Mathematics concerned with questions of shape, size, relative position of figures, and the properties of space.
In Mathematics and Physics, the dimensions of a space or object are informally defined in Euclidian Geometry (see below) as the minimum number of coordinates needed to specify any Point within it (Point P in the illustration below).
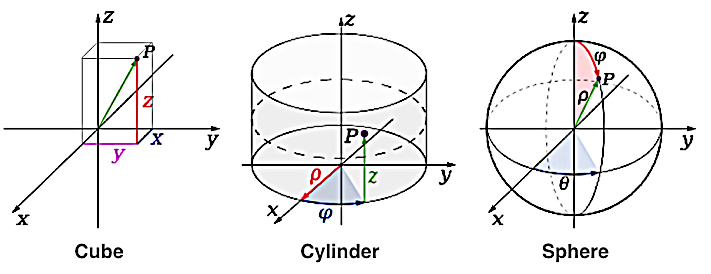
Thus the inside of a Cube, a Cylinder or a Sphere is in a 3-Dimensional Space because 3 coordinates - X,Y and Z - are needed to locate a Point within these Spaces.
The method of describing the location of Points was proposed by the French mathematician René Descartes (1596 - 1650). He proposed further that curves and lines could be described by equations using this technique. He was the first to link Algebra and Geometry. In honor of his work, the coordinates of a Point are often referred to as its Cartesian coordinates, and the coordinate plane as the Cartesian Coordinate Plane.
The basic Dimensions of Dimensional Spaces are:
- 0-Dimension: a Point.
- 1-Dimension Space: a Line (a Line is made of Points).
- 2-Dimension Space: a Surface (a Surface is made of Lines).
- 3-Dimensions Space: a Volume (a Volume is made of Surfaces).
Euclidian Geometry
Euclidian Geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid. He described it in his textbook on geometry: the Elements.
Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions or theorems from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system.
Non-Euclidian Geometry
Einstein's Theory of General Relativity shows that the true geometry of Spacetime is Non-Euclidean Geometry. For example, if a triangle is constructed out of three rays of light, then in general the interior angles do not add up to 180 degrees due to gravity. A relatively weak gravitational field, such as the Earth's or the sun's, is represented by a metric that is approximately, but not exactly, Euclidean. Until the 20th century, there was no technology capable of detecting the deviations from Euclidean Geometry, but Einstein predicted that such deviations would exist. They were later verified by observations such as the slight bending of starlight by the sun during a solar eclipse in 1919, and such considerations are now an integral part of the software that runs the GPS systems.
2 & 3 Dimensions
Dimensional Objects
The Euclidian Geometry is extended to 4-Dimensional Geometry by adding one additional Dimension that is NOT Time. Hence the prefix "Hyper" is often used to refer to Objects in Dimensions higher than 3.
3D 2D Geometry is however limiting its scope to 2 and 3 Dimensions.
The Table below provides a list of the most common names of 2 to 4 Dimensional Objects:
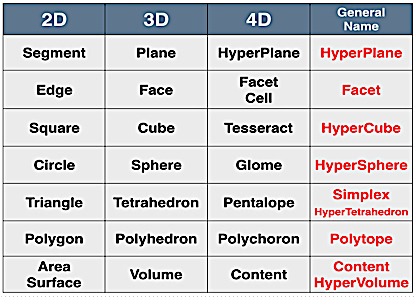
NOTE: A temporal Dimension is a Dimension of Time. Time is often referred to as the "4th dimension" for this reason, but that is NOT to imply that it is a Spatial Dimension. A temporal Dimension is one way to measure physical change. It is perceived differently from the 3-Dimensional Space in that there is only one of it, and that we cannot move freely in Time but subjectively move in one direction.
The Spacial Dimensions 1, 2, 3 that are the building block of the basic geometry are:


Higher Dimensions
Although the notion of higher Dimensions goes back to René Descartes, substantial development of a higher-dimensional geometry only began in the 19th century, through the work of Arthur Cayley, William Rowan Hamilton, Ludwig Schläfli that marked the beginning of higher-dimensional geometry.
Theoretically, it is possible to extend the progression of Dimensions to include 4-Dimensional shapes such as Tesseracts and Hyper-Spheres, 5-Dimensional ones, and so on up to an infinite number of dimensions.
Although human beings have only immediate experience of the 3-Dimensional Space, this does not rule out at all the existence of other higher-numbered ones called Hyper-Spaces, the 4-Dimensional Space being one of them. It is of particular interest.
The Fourth Dimension in the 4-Dimension Space is NOT TIME, NOTSpacetime, but Space; not outer Space, but another spatial direction which extends in a direction perpendicular to all directions we are familiar with in our 3-Dimension Space or World or Universe.
When you think of the 4-Dimension Space as being an extension of Space, the best way to visualize this is to imagine a bunch of 3-Dimension Spaces (or worlds) “stacked” on each other.
The 4-Dimensional Space has 4 independent directions. A dimension is a direction that an object that moves in the space will follow.

Since our world is in 3 Dimensions we can only get partial representations of the 4-Dimensional Space. By intuition we somewhat understand what it is. For example when a 4-Dimension object goes through our 3-Dimension space we only see partial slices of it, but never the full 4-Dimension object.
In Science Fiction:
- In Madeleine L'Engle's novel "A Wrinkle in Time" the characters in the story travel through Time and Space using Tesseracts (Hypercube). The book uses the word "tesser" to refer to movement from one three dimensional space/world to another).
- In the science fiction novel "Factoring Humanity" by Robert J. Sawyer, a Tesseract is used by humans on Earth to enter the fourth dimension and contact another civilization on a planet orbiting the star Alpha Centauri A. The hypercube initially exists as a series of connected 3-dimensional cubes, which represent a hypercube that has been unfolded. Refolding the cube in a certain specific manner causes the reformation of the hypercube in 4 dimensions.
Today many other non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's Theory of General Relativity is that physical space itself is not Euclidean, and the Euclidean space is a good approximation for it only where the gravitational field is weak.
Over the years Scientists and Physicists have attempted to unify a number of theories with various degree of success. Does Quantum Gravity exist and can be proven?
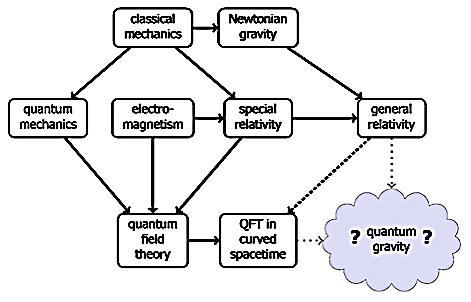
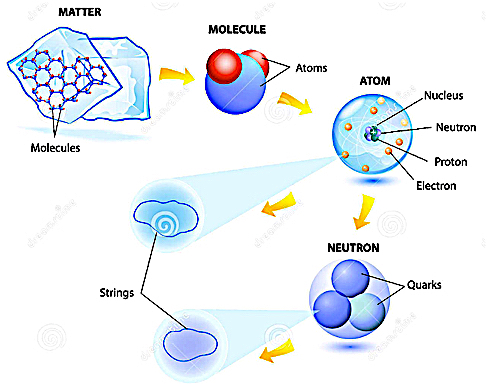
String Theory
In physics, String Theory is a theoretical framework in which the point-like particles of particle physics are replaced by 1-Dimensional objects called Strings. The theory describes how these Strings propagate through space and interact with each other. On distance scales larger than the string scale, a string looks just like an ordinary particle, with its mass, charge, and other properties determined by the vibrational state of the string. In string theory, one of the many vibrational states of the string corresponds to the graviton, a quantum mechanical particle that carries gravitational force. The String Theory is therefore a theory of Quantum Gravity.